Tensorflow - part 3: Automatic differentiation

Posted 7. September 2021. 14 min read.

Automatic differentiation is very handy for running backpropagation when training neural networks.

Let's import necessary packages

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf

tf.GradientTape

tf.GradientTape is an API for automatic differentiation. For this API to do the differentiation automatically in the backward phase, the included operations and the order to operate them in the forward pass needs to be known.

tensor_x = tf.Variable(2.0) # x: a Tensorflow variable of scalar

with tf.GradientTape() as tape: # Tensorflow remembers all the executed operations in ```tf.GradientTape``` by storing them into a ```tape```
  tensor_y1 = tensor_x**2 # y1
  tensor_y2 = tensor_x**3 # y2

Tensorflow remembers all the executed operations in tf.GradientTape by storing them into a tape.

To calculate the gradient of some targets with respect to some sources, use tape.gradient(target, source). For example, to calculate the differentiation of y1 with respect to x.

tensor_dy1_dx = tape.gradient(tensor_y1, tensor_x) # dy = 2x dx
print(tensor_dy1_dx)

Output

tf.Tensor(4.0, shape=(), dtype=float32)

We know that dy1 = 2x dx. If x = 2, then dy1/dx = 4, which is correct.

Now, try again with the differentiation of y2 with respect to x.

tensor_dy2_dx = tape.gradient(tensor_y2, tensor_x) # dy = 3x^2 dx
print(tensor_dy2_dx)

Output

RuntimeError: A non-persistent GradientTape can only be used to compute one set of gradients (or jacobians)

There will be a Runtime error like above. Because the GradientTape.gradient() method can only be called once and then the resources in the GradientTape are released. A persistent gradient tape is the solution for calling gradient() multiple times. Only when the tape object is garbage-collected does Tensorflow release the resources.

Persistent tape

To have a persistent tape, set the argument persistent to True (persistent = True). Run the below code to verify.

with tf.GradientTape(persistent=True) as tape:
  tensor_y1 = tensor_x**2
  tensor_y2 = tensor_x**3
  tensor_y3 = 4*tensor_x + 1

# To calculate the gradient of some target with respect to some source
tensor_dy1_dx = tape.gradient(tensor_y1, tensor_x) # dy = 2x dx 
tensor_dy2_dx = tape.gradient(tensor_y2, tensor_x) # dy = 3x^2 dx
tensor_dy3_dx = tape.gradient(tensor_y3, tensor_x) # dy = 4 dx
print(tensor_dy1_dx)
print(tensor_dy2_dx)
print(tensor_dy3_dx)

Output

The tensor_x is assigned with value 2 above, so the results are:

tf.Tensor(4.0, shape=(), dtype=float32)
tf.Tensor(12.0, shape=(), dtype=float32)
tf.Tensor(4.0, shape=(), dtype=float32)

Remember to delete tape after using.

del tape

Conditions to use `tf.GradientTape.gradient()`

Suppose we need to calculate a simple linear equation y = x*w + b.

First initialize a tensor_w of shape (4, 3) with random uniform values and a tensor_b of shape (3,).

tf.random.set_seed(1)
tensor_w = tf.Variable(tf.random.uniform((4, 3), minval=-20, maxval=20, dtype=tf.float32), name='w') # w: weight
tensor_b = tf.Variable(tf.ones(3, dtype=tf.float32), name='b') # bias
print(tensor_w)

Output

<tf.Variable 'w:0' shape=(4, 3) dtype=float32, numpy=
array([[-13.394766 ,  16.05925  ,   5.238968 ],
       [ -2.6181564,  -8.322439 ,   5.700083 ],
       [ 19.031418 ,  -2.5960197,   6.4040756],
       [  4.195833 ,   5.4652596,   4.5779514]], dtype=float32)>

Next, we temporarily delay the appearance of tensor_x for the later part as we need to point out some important notes through assigning it with different values on the right side of the equal sign.

The tf.GradientTape is defined as:

with tf.GradientTape(persistent=True) as tape:
  # tape.watch(tensor_x) # Let's comment this for now. We will explain later for this tape.watch()
  tensor_y = tensor_x @ tensor_w + tensor_b # @ is matrix multiplication
  tensor_loss = tf.reduce_mean(tensor_y**2) # dloss = mean(2*y) dy; dloss = (2*y[0] + 2*y[1] + 2*y[2])/3

print('[+] tensor_y: ', tensor_y)
print('[+] tensor_loss: ', tensor_loss)

All the operations inside the with tf.GradientTape(persistent=True) as tape: are said to be in the GradientTape context.

Next is the gradient calculation part.

tensor_dy_dx = tape.gradient(tensor_y, tensor_x)
tensor_dloss_dy = tape.gradient(tensor_loss, tensor_y) # source tensor_y has 3 elements, so there will be 3 derivative: dloss/dy[0] = 2*y[0]/3, dloss/dy[1]=2*y[1]/3, dloss/dy[2]=2*y[2]/3
tensor_dloss_dx = tape.gradient(tensor_loss, tensor_x)

print('[+] tensor_dy_dx: ', tensor_dy_dx)
print('[+] tensor_dloss_dy: ', tensor_dloss_dy)
print('[+] tensor_dloss_dx: ', tensor_dloss_dx)

Now is the time to define tensor_x. In the code below, tensor_x is assigned 5 times. They differ in some ways: whether tf.Variable or tf.constant are used?, trainable is set to True or False?, dtype is set to int or float?, is there any operation with a constant following the tf.Variable definition. We will try assigning tensor_x with one of the 5 types one-by-one and see what happens.

tensor_x = tf.Variable([[1, 2, 3, 4]], dtype=tf.float32, name='x') # Case 1
tensor_x = tf.Variable([[1, 2, 3, 4]], dtype=tf.int32, name='x') # Case 2. Note that in this case, tensor_w and tensor_b are also converted to type tf.int32
tensor_x = tf.Variable([[1, 2, 3, 4]], dtype=tf.float32, trainable=False) # Case 3
tensor_x = tf.constant([[1, 2, 3, 4]], dtype=tf.float32) # Case 4
tensor_x = tf.Variable([[1, 2, 3, 4]], dtype=tf.float32, name='x') + 1.0 # Case 5

Next, we show the outputs for each case of tensor_x:

Output

You should find the differences between the cases on your own before we reveal them below. Cues: there are several calculations resulting in None. Why? Many reasons ...

Case 1:
[+] tensor_y:  tf.Tensor([[56.246506 14.48735  55.163166]], shape=(1, 3), dtype=float32)
[+] tensor_loss:  tf.Tensor(2138.8425, shape=(), dtype=float32)
[+] tensor_dy_dx:  tf.Tensor([[ 7.903452 -5.240513 22.839474 14.239044]], shape=(1, 4), dtype=float32)
[+] tensor_dloss_dy:  tf.Tensor([[37.497673  9.658234 36.775444]], shape=(1, 3), dtype=float32)
[+] tensor_dloss_dx:  tf.Tensor([[-154.50319    31.068237  924.07367   378.47495 ]], shape=(1, 4), dtype=float32)

Case 2:
[+] tensor_y:  tf.Tensor([[ -5 103 -64]], shape=(1, 3), dtype=int32)
[+] tensor_loss:  tf.Tensor(4910, shape=(), dtype=int32)
[+] tensor_dy_dx:  None
[+] tensor_dloss_dy:  None
[+] tensor_dloss_dx:  None

Case 3:
[+] tensor_y:  tf.Tensor([[56.246506 14.48735  55.163166]], shape=(1, 3), dtype=float32)
[+] tensor_loss:  tf.Tensor(2138.8425, shape=(), dtype=float32)
[+] tensor_dy_dx:  None
[+] tensor_dloss_dy:  tf.Tensor([[37.497673  9.658234 36.775444]], shape=(1, 3), dtype=float32)
[+] tensor_dloss_dx:  None

Case 4:
[+] tensor_y:  tf.Tensor([[56.246506 14.48735  55.163166]], shape=(1, 3), dtype=float32)
[+] tensor_loss:  tf.Tensor(2138.8425, shape=(), dtype=float32)
[+] tensor_dy_dx:  None
[+] tensor_dloss_dy:  tf.Tensor([[37.497673  9.658234 36.775444]], shape=(1, 3), dtype=float32)
[+] tensor_dloss_dx:  None

Case 5:
[+] tensor_y:  tf.Tensor([[63.46084  25.093401 77.08424 ]], shape=(1, 3), dtype=float32)
[+] tensor_loss:  tf.Tensor(3532.9792, shape=(), dtype=float32)
[+] tensor_dy_dx:  None
[+] tensor_dloss_dy:  tf.Tensor([[42.307224 16.728935 51.389496]], shape=(1, 3), dtype=float32)
[+] tensor_dloss_dx:  None

Do you remember the line tape.watch(tensor_x) which is commented out in the above code of tf.GradientTape context? Now let's uncomment it and try again with the 5 cases of tensor_x:

with tf.GradientTape(persistent=True) as tape:
  tape.watch(tensor_x) # Uncomment this line 
  tensor_y = tensor_x @ tensor_w + tensor_b # @ is matrix multiplication
  tensor_loss = tf.reduce_mean(tensor_y**2) # dloss = mean(2*y) dy; dloss = (2*y[0] + 2*y[1] + 2*y[2])/3

then the outputs are:

Output

You definitely see that there are less None values than above. Some gradient calculations having tensor_x (dx) as source have transformed from None to a value. That is because the tensor_x have been watched by the GradientTape, so the gradients with respect to this variable are now valid.

Case 1:
[+] tensor_y:  tf.Tensor([[56.246506 14.48735  55.163166]], shape=(1, 3), dtype=float32)
[+] tensor_loss:  tf.Tensor(2138.8425, shape=(), dtype=float32)
[+] tensor_dy_dx:  tf.Tensor([[ 7.903452 -5.240513 22.839474 14.239044]], shape=(1, 4), dtype=float32)
[+] tensor_dloss_dy:  tf.Tensor([[37.497673  9.658234 36.775444]], shape=(1, 3), dtype=float32)
[+] tensor_dloss_dx:  tf.Tensor([[-154.50319    31.068237  924.07367   378.47495 ]], shape=(1, 4), dtype=float32)

Case 2:
[+] tensor_y:  tf.Tensor([[ -5 103 -64]], shape=(1, 3), dtype=int32)
[+] tensor_loss:  tf.Tensor(4910, shape=(), dtype=int32)
[+] tensor_dy_dx:  None
[+] tensor_dloss_dy:  None
[+] tensor_dloss_dx:  None

Case 3:
[+] tensor_y:  tf.Tensor([[56.246506 14.48735  55.163166]], shape=(1, 3), dtype=float32)
[+] tensor_loss:  tf.Tensor(2138.8425, shape=(), dtype=float32)
[+] tensor_dy_dx:  tf.Tensor([[ 7.903452 -5.240513 22.839474 14.239044]], shape=(1, 4), dtype=float32)
[+] tensor_dloss_dy:  tf.Tensor([[37.497673  9.658234 36.775444]], shape=(1, 3), dtype=float32)
[+] tensor_dloss_dx:  tf.Tensor([[-154.50319    31.068237  924.07367   378.47495 ]], shape=(1, 4), dtype=float32)

Case 4:
[+] tensor_y:  tf.Tensor([[56.246506 14.48735  55.163166]], shape=(1, 3), dtype=float32)
[+] tensor_loss:  tf.Tensor(2138.8425, shape=(), dtype=float32)
[+] tensor_dy_dx:  tf.Tensor([[ 7.903452 -5.240513 22.839474 14.239044]], shape=(1, 4), dtype=float32)
[+] tensor_dloss_dy:  tf.Tensor([[37.497673  9.658234 36.775444]], shape=(1, 3), dtype=float32)
[+] tensor_dloss_dx:  tf.Tensor([[-154.50319    31.068237  924.07367   378.47495 ]], shape=(1, 4), dtype=float32)

Case 5:
[+] tensor_y:  tf.Tensor([[63.46084  25.093401 77.08424 ]], shape=(1, 3), dtype=float32)
[+] tensor_loss:  tf.Tensor(3532.9792, shape=(), dtype=float32)
[+] tensor_dy_dx:  tf.Tensor([[ 7.903452 -5.240513 22.839474 14.239044]], shape=(1, 4), dtype=float32)
[+] tensor_dloss_dy:  tf.Tensor([[42.307224 16.728935 51.389496]], shape=(1, 3), dtype=float32)
[+] tensor_dloss_dx:  tf.Tensor([[ -28.813324   42.9319   1090.8401    504.20065 ]], shape=(1, 4), dtype=float32)

tape.watch() is needed when tensor_x is a tensor, not Variable. watch is used to trace tensor by tape.

From doing the two experiments above, we can infer that there are 3 cases of tensor_x that we need to use tape.watch:

When trainable=False, need to use tape.watch to calculate gradients with respect to this Variable.
When use tensor (not tf.Variable), need to use tape.watch to calculate gradients with respect to this tensor.
When a tf.Variable is added with a number or a tensor (or other operations), it becomes a tensor. So, to calculate gradients with respect to it we also need to use tape.watch.

Overall, the tensor_x and the related tensors in the process of calculating gradient need to be a tf.Variable, not a tensor (although tf.Variable is also a special type of tensor, except its elements can be changed). Moreover, all the ingredient tensors must be float type (int and string type will not work).

One useful habit is that you should always check if a target or a source is of type tf.Variable before running tape.gradient.

Source as list, dictionary; target as dictionary

Consider the case 1 of tensor_x.

Multiple sources:

The source can also be passes as a list of variables. tape.gradient will calculate differentiation with respect to each of them.

tensor_dloss_dw, tensor_dloss_db = tape.gradient(tensor_loss, [tensor_w, tensor_b])

print('[+] tensor_dloss_dw: ', tensor_dloss_dw)
print('[+] tensor_dloss_db: ', tensor_dloss_db)

Output

[+] tensor_dloss_dw:  tf.Tensor(
[[ 37.497673   9.658234  36.775444]
 [ 74.995346  19.316467  73.55089 ]
 [112.49302   28.9747   110.32633 ]
 [149.99069   38.632935 147.10178 ]], shape=(4, 3), dtype=float32)

[+] tensor_dloss_db:  tf.Tensor([37.497673  9.658234 36.775444], shape=(3,), dtype=float32)

Or a source can even be a dictionary.

dic_vars = {
    'tensor_w': tensor_w,
    'tensor_b': tensor_b
}
tensor_dloss_dwdb_dic = tape.gradient(tensor_loss, dic_vars)

print('[+] tensor_dloss_dw_dic: ', tensor_dloss_dwdb_dic['tensor_w'])
print('[+] tensor_dloss_db_dic: ', tensor_dloss_dwdb_dic['tensor_b'])

Output

[+] tensor_dloss_dw_dic:  tf.Tensor(
[[ 37.497673   9.658234  36.775444]
 [ 74.995346  19.316467  73.55089 ]
 [112.49302   28.9747   110.32633 ]
 [149.99069   38.632935 147.10178 ]], shape=(4, 3), dtype=float32)

[+] tensor_dloss_db_dic:  tf.Tensor([37.497673  9.658234 36.775444], shape=(3,), dtype=float32)

Multiple targets:

Gradients of multiple targets. This is not like the case of multiple sources where tape.gradient calculates gradients separately with respect to each source.

Here, the gradient of multiple targets = the gradient of the sum of the targets = the sum of the gradients of all targets

tensor_dydloss_dx = tape.gradient({'tensor_y': tensor_y, 'tensor_loss': tensor_loss}, tensor_x)

print('[+] tensor_dydloss_dx: ', tensor_dydloss_dx)

Output

[+] tensor_dydloss_dx:  tf.Tensor([[-146.5997    25.82772  946.9131   392.71396]], shape=(1, 4), dtype=float32)
['w:0', 'b:0', 'x:0']

Until now, you may also notice that the gradient result tensor has the same shape as the source tensor (in tape.gradient(target, source)). You can verify it by the code below. We just take some gradients for example.

print(tensor_x.shape) # source
print(tensor_dy_dx.shape) # gradient
print(tensor_y.shape) # source
print(tensor_dloss_dy.shape) # gradient
print(tensor_w.shape) # source
print(tensor_dloss_dw.shape) # gradient
print(tensor_b.shape) # source
print(tensor_dloss_db.shape) # gradient

Output

(1, 4)
(1, 4)
(1, 3)
(1, 3)
(4, 3)
(4, 3)
(3,)
(3,)

See which variables are watched by `tape`

We look in tape.watched_variables()

print('[+] watched variables: ', [watched_var.name for watched_var in tape.watched_variables()])

We also check for the 5 cases of tensor_x when tape.watch(tensor_x) is used.

Output

Case 1:
[+] watched variables:  ['w:0', 'b:0', 'x:0']

Case 2:
[+] watched variables:  ['w:0', 'b:0', 'x:0']

Case 3:
[+] watched variables:  ['w:0', 'b:0', 'Variable:0'] # tensor_x is not named as "x"

Case 4:
[+] watched variables:  ['w:0', 'b:0']

Case 5:
[+] watched variables:  ['w:0', 'b:0']

In case 4 and case 5, there is no variable of tensor_x because as we know, tape.watch just "locally watches" tensor_x in the tf.GradientTape context.

Checking which operations are stored for the backward propagation

Or this process can also be thought as checking which variables are trainable. Let's create a simple neural network to check this.

layer1 = tf.keras.layers.Dense(2, activation='relu', name="dense_1")
# The calculation of Dense is: output = activation(dot(input, kernel) + bias)
layer2 = tf.keras.layers.Dense(4, activation='relu', name="dense_2")
# In ```Dense`` by defaults, kernel is initialized according to glorot uniform and bias is initialized with zeros
tensor_x = tf.constant([[1., 2., 3.]])

with tf.GradientTape(persistent=True) as tape:
  # Forward pass
  tensor_h = layer1(tensor_x)
  tensor_y = layer2(tensor_h)
  tensor_loss = tf.reduce_mean(tensor_y**2)

# Calculate gradients with respect to each trainable variables
print('[+] The trainable vairables of layer1: ', layer1.trainable_variables)
print('[+] The trainable vairables of layer2: ', layer2.trainable_variables)
tensor_dloss_dvars_layer1 = tape.gradient(tensor_loss, layer1.trainable_variables)
tensor_dloss_dvars_layer2 = tape.gradient(tensor_loss, layer2.trainable_variables)

print("Dense 1:")
for var, grad in zip(layer1.trainable_variables, tensor_dloss_dvars_layer1):
  print('[+] variable name, shape: {0}, {1}'.format(var.name, grad.shape)) # The shape of gradient is the same as the shape of source

print("Dense 2:")
for var, grad in zip(layer2.trainable_variables, tensor_dloss_dvars_layer2):
  print('[+] variable name, shape: {0}, {1}'.format(var.name, grad.shape)) # The shape of gradient is the same as the shape of source

Output

[+] The trainable vairables of layer1:  [<tf.Variable 'dense_1/kernel:0' shape=(3, 2) dtype=float32, numpy=
array([[-0.57740456, -0.572319  ],
       [ 0.00795567,  0.5992962 ],
       [ 0.24269533,  0.8154019 ]], dtype=float32)>, <tf.Variable 'dense_1/bias:0' shape=(2,) dtype=float32, numpy=array([0., 0.], dtype=float32)>]
[+] The trainable vairables of layer2:  [<tf.Variable 'dense_2/kernel:0' shape=(2, 4) dtype=float32, numpy=
array([[ 0.46956396, -0.71557474, -0.8732331 , -0.62160015],
       [ 0.59634185,  0.40849257, -0.18213058,  0.02854967]],
      dtype=float32)>, <tf.Variable 'dense_2/bias:0' shape=(4,) dtype=float32, numpy=array([0., 0., 0., 0.], dtype=float32)>]
Dense 1:
[+] variable name, shape: dense_1/kernel:0, (3, 2)
[+] variable name, shape: dense_1/bias:0, (2,)
Dense 2:
[+] variable name, shape: dense_2/kernel:0, (2, 4)
[+] variable name, shape: dense_2/bias:0, (4,)

When using gradient tapes, memory are used to store all the results which are required for the backward propagation. There are some unnecessary operations such as ReLU are removed during the forward pass.

Control flow/Choose scope for assigning variable by if

We can use if to choose which variable is assigned to a final result. Therefore, only calculating gradient according to the chosen one is possible. See the example below for more details.

Have a code like this. Either tensor_x1 or tensor_x2 is used to assign the tensor_res_1, which depends on the if condition.

tensor_x1 = tf.Variable(3.0)
tensor_x2 = tf.Variable(3.0)

tensor_flag = tf.constant(2.0) # a tensor to use in the if condition; must be float

with tf.GradientTape(persistent=True) as tape:
  tape.watch(tensor_x1)
  tape.watch(tensor_x2)
  tape.watch(tensor_flag)
  if tensor_flag % 2 == 0:
    tensor_res_1 = 4*(tensor_x1**2) + 3
  else:
    tensor_res_1 = tensor_x2**3

tensor_dres1_dx1, tensor_dres1_dx2 = tape.gradient(tensor_res_1, [tensor_x1, tensor_x2])
print('[+] tensor_dres1_dx1: ', tensor_dres1_dx1)
print('[+] tensor_dres1_dx2', tensor_dres1_dx2)

Output

[+] tensor_dres1_dx1:  tf.Tensor(24.0, shape=(), dtype=float32)
[+] tensor_dres1_dx2 None

Because tensor_flag % 2 == 0, tensor_res_1 is assigned with 4*(tensor_x1**2) + 3. Therefore, we can only calculate the gradient with respect to tensor_x1.

Let's try with one more experiment. Here we have one more variable to assign tensor_res_2. This assignation depends on out last work of tensor_res_1. If tensor_res_1 is assigned with the function 4*(tensor_x1**2) + 3, then tensor_res_2 will be assigned with the other and in reverse.

with tf.GradientTape(persistent=True) as tape2:
  tape2.watch(tensor_x1)
  tape2.watch(tensor_x2)
  
  if tf.math.equal(tensor_res_1, 4*(tensor_x1**2) + 3).numpy().all():
    tensor_res_2 = tensor_x2**3
  else:
    tensor_res_2 = 4*(tensor_x1**2) + 3

tensor_dres2_dx1, tensor_dres2_dx2 = tape2.gradient(tensor_res_2, [tensor_x1, tensor_x2]) # Remember to use ```tape2.gradient()``` here, not ```tape.gradient()```. Otherwise, the gradient results will not be as expected.
print('[+] tensor_dres2_dx1: ', tensor_dres2_dx1)
print('[+] tensor_dres2_dx2', tensor_dres2_dx2)

Output

[+] tensor_dres2_dx1:  None
[+] tensor_dres2_dx2 tf.Tensor(27.0, shape=(), dtype=float32)

In this second experiment, we need to use another name for tape (tape2) so it can be discriminated with the one above and used as a completely different gradient context.

tf.math.equal is used to element-wise check if all the elements of tensor_res and 4*(tensor_x1**2) + 3 are equal. It will return an array of boolean values each of which corresponds to a comparison result of a pair. Then we should use all() to check if all the boolean values are True.

Let's also check what happens if we use tape.gradient (not tape2.gradient) for tensor_res_2.

tensor_dres2_dx1_tmp, tensor_dres2_dx2_tmp = tape.gradient(tensor_res_2, [tensor_x1, tensor_x2])

print('[+] tensor_dres2_dx1_tmp: ', tensor_dres2_dx1_tmp) # None. Is that because ```tensor_x1``` is not assigned to ```tensor_res_2```? Not exactly, it is because in the context of ```tape`` does not exist the ```tensor_res_2```
print('[+] tensor_dres2_dx2_tmp: ', tensor_dres2_dx2_tmp) # None. The same reason as above.

Output

[+] tensor_dres2_dx1_tmp:  None
[+] tensor_dres2_dx2_tmp: None

Both of the printings are None.

The first None: Is that because tensor_x1 is not assigned to tensor_res_2? Not exactly, it is because in the context of tape does not exist the tensor_res_2.
The second None: The same reason as the first None.

Plot a function and its gradient

To plot a function, we need many values of x. Get the codes in the previous section as example with one change. Instead of assigning tensor_x1 and tensor_x2 each with a single value, now we assign each of them with a list of values by using tf.linspace.

tensor_x1 = tf.linspace(-15.0, 15.0, 150+1)
tensor_x2 = tf.linspace(-15.0, 15.0, 150+1)

With each value of tensor_x1 (or tensor_x2), there will be a corresponding function value and its gradient value. With these values, now we can plot these functions.

Plot the function tensor_res_1 and its gradient with respect to x1 tensor_dres1_dx1

plt.plot(tensor_x1, tensor_res_1, label='res1')
plt.plot(tensor_x1, tensor_dres1_dx1, label='dres1')
plt.legend()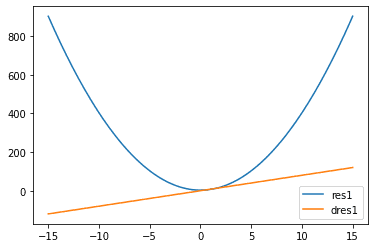

Plot the function tensor_res_2 and its gradient with respect to x2 tensor_dres2_dx2

plt.plot(tensor_x2, tensor_res_2, label='res2')
plt.plot(tensor_x2, tensor_dres2_dx2, label='dres2')
plt.legend()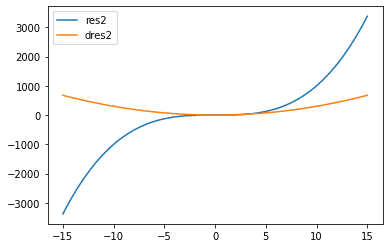

Some more things to notice

According to Tensorflow autodiff guide, There are 2 more essential things to notice:

There are some tensorflow operations (tf.Operation) that are registered as being non-differentiable or have no gradient registered (differentiable but have not been registered). For the latter case, if you need to make differentiation on this type of operation, there are 2 options:
- Implement the the gradient and register it (using tf.RegisterGradient).
- Re-implement the function using other ops.
Sometimes, it is better to return zeros rather than None. To do this, add the argument unconnected_gradients=tf.UnconnectedGradients.ZERO to the function tape.gradient()

The end

AI and Software Development enthusiasts. Knowledge is common. Our insights and experience on it is unique

Tensorflow - part 3: Automatic differentiation

tf.GradientTape

Persistent tape

Conditions to use tf.GradientTape.gradient()

Source as list, dictionary; target as dictionary

Multiple sources:

Multiple targets:

See which variables are watched by tape

Checking which operations are stored for the backward propagation

Control flow/Choose scope for assigning variable by if

Plot a function and its gradient

Some more things to notice

The end

Conditions to use `tf.GradientTape.gradient()`

See which variables are watched by `tape`